Atmospheric Ionizing Radiation
I. Introduction


This report describes the radiation environment in the atmosphere, and an empirical model used to calculate absorbed dose rate within this environment as a function of altitude and geomagnetic location. This study complements the student education/outreach portion of a recent NASA EPSCoR grant that measures absorbed dose rate from cosmic radiation at altitudes up to approximately 100k feet using inexpensive ionization chambers flown on standard weather balloons. A simple computer program called Atmospheric Ionizing Radiation (AIR) verifies the results from such flights. This empirical model calculates absorbed dose rate based on the following considerations: time; latitude; longitude; altitude; galactic cosmic ray (GCR) spectrum; ionization rate; neutron contribution; geomagnetic field and cutoff; solar cycle phase.
The AIR model was modified to make use of neutron count rates and vertical cutoff rigidities provided by the Climax Neutron Monitor in Colorado, the nearest operating neutron monitor to Stillwater, Oklahoma. In this report, we describe this model and show comparisons with actual balloon flight data.
The radiation environment within the Earth's atmosphere is complex and changes with altitude, geomagnetic position, and time. The radiation environment is dominated by cosmic radiation at all but the lowest altitudes. This is not due to primary cosmic radiation, but rather cosmic ray secondaries produced through nuclear interactions. These secondary particles are the result of air showers or particle cascades initiated when primary cosmic rays interact with the constituent nuclei of the atmosphere. An understanding of the radiation environment at high altitudes can be obtained by considering the sources of cosmic radiation and the different physical processes that affect this radiation. For high altitudes, one must first consider propagation of this radiation field through the Earth's magnetosphere before taking into account its propagation in the atmosphere.
For the most part, life is shielded against this radiation by approximately 1,033 g/cm2 of air, which is comparable to a water depth of roughly 10 m. On the ground, cosmic rays contribute less than 10% of the total absorbed dose rate of natural background radiation. While not a health issue on the ground, exposure to cosmic radiation may be a health concern at altitudes greater than 30k ft. At these altitudes, airline pilots and flight attendants are considered radiation workers since they can accumulate a biologically-weighted absorbed dose of approximately 9 mSv/yr, assuming 600 hr/yr exposure time. This is compared to approximately 0.3 mSv/yr for the average person at sea level. Prolonged exposure to high altitude cosmic radiation may increase the risk of fatal cancer as well as the development of cataracts in the eyes. Exposure to ionizing radiation can also adversely affect aircraft electronics (avionics). In addition to practical concerns, atmospheric ionizing radiation is part of our environment and thus intrinsically interesting.
II. Radiation Environment in the Atmosphere


Interaction of GCRs with the Interplanetary Medium
Galactic cosmic rays (GCRs) are charged particles that originate from sources beyond our solar system. At least outside of the heliosphere, the distribution of GCRs is believed to be isotropic throughout interstellar space. The energy range of GCRs varies considerably, from a few tens of MeV/nucleon to as high as 1016 MeV/nucleon. The total flux of GCRs is very low, being about 0.53 (cm2‑sec‑sr)-1 near solar minimum, and about half that value near solar maximum. This illustrates the effect of the solar cycle, which indirectly modulates the flux of high energy GCRs entering the solar system via the solar wind. The solar cycle is an 11-year periodic trend in the number of sunspots visible on the surface of the Sun and is indicative of solar activity. The GCR spectrum consists of two main components: baryonic and leptonic. The baryon component is composed of 98% protons and heavy ions. A heavy ion refers to an ionized atom which is usually heavier than beryllium ($Z$ = 4). The lepton component makes up the remaining 2% with electrons and positrons. The 98% baryon portion of the spectrum is broken down as follows:
- 87% protons;
- 12% helium ions (alpha particles);
- 1% heavy ions with atomic numbers ranging from $Z$ = 3 (Li) to 92 (U).
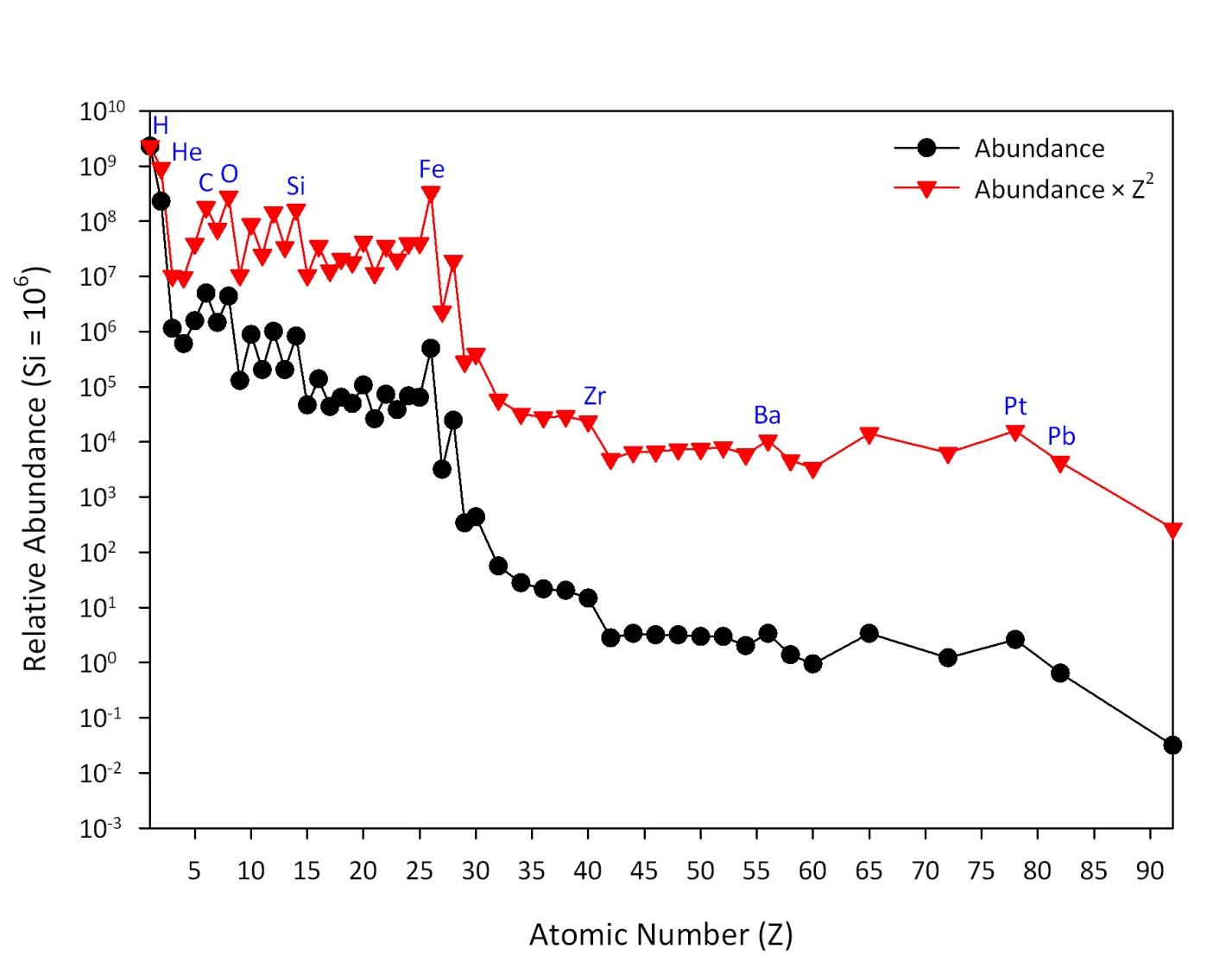
Highly energetic particles in the heavy ion component, or HZE particles, are important from a radiobiological standpoint because they possess a high linear energy transfer (LET) and are highly penetrating. LET is the amount of energy deposited per unit path length of a charged particle on transit through a medium (units: keV/μm). Figure 2.1 shows relative abundances of various GCR species both as a function of $Z$ and $Z^2$. The fundamental dosimetric quantity of absorbed dose, in units of gray (Gy = gray; 1 Gy = 1 J/kg), is proportional to LET, and LET is proportional to $Z^2$. Energetic iron nuclei are the most important HZE particles, as Figure 2.1 demonstrates, since they are relatively plentiful compared to other high $Z$ particles.
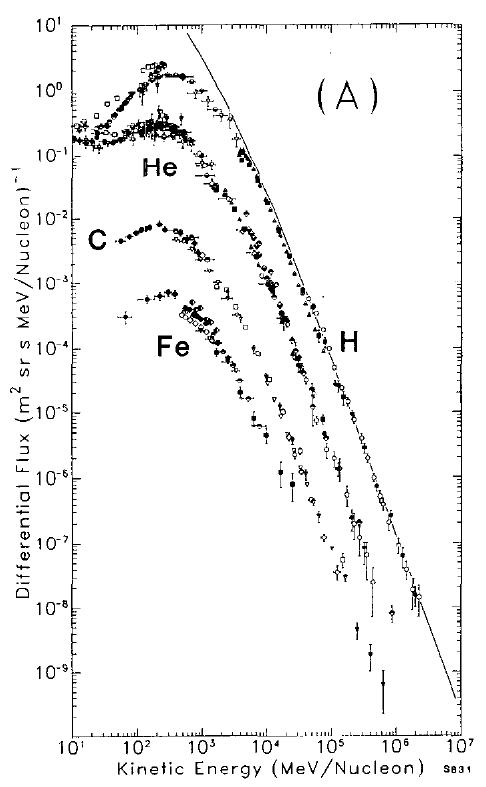
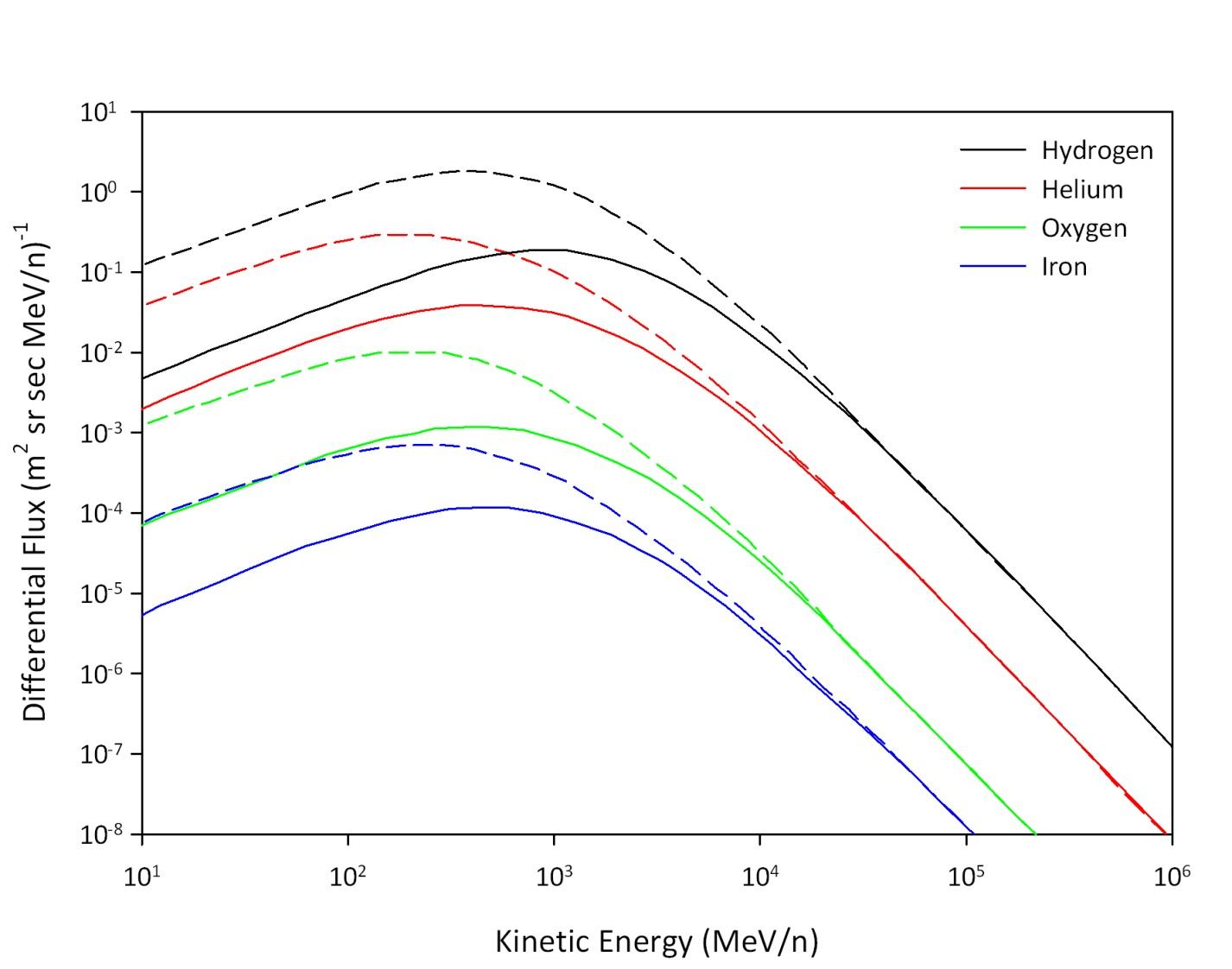
Figure 2.2 shows the measured energy spectra of various components of the GCR spectrum [8]. The general shape of the observed differential energy spectra in this plot is typical of measurements at the orbit of Earth. Figure 2.3 details the attenuating effect of solar activity on the GCR spectrum via a model calculation. This model contains improvements in the treatment of the time-dependent solar adjustment of the GCR spectrum. This improved treatment predicts that the flux is relatively insensitive to variables such as solar wind velocity. However, the large scale structure of the interplanetary magnetic field (IMF) is important, which the solar wind transports. The solar wind is a stream of charged particles that is electrically conductive so that magnetic field lines from the Sun are carried along with it. The solar wind creates the heliosphere, which can be thought of as a vast "bubble" in the interstellar medium surrounding the solar system. The lower energy component of the GCR flux entering the heliosphere is partially attenuated as these particles are scattered by irregularities in the IMF embedded in the solar wind. The large scale structure of the IMF changes in shape through the 11-year solar cycle, causing variations in the GCR spectrum over solar maximum and minimum as shown by Figure 2.3. In general, the changes in the spectra of Figure 2.3 are indirect responses to the level of solar activity that is manifested in the large scale changes of the IMF carried by the solar wind.
Interaction of GCRs with the Earth's Magnetic Field
Since GCRs are charged particles, they are affected by the Earth's magnetic field. These charged particles tend to follow lines of the geomagnetic field, which are parallel to the Earth's surface near the equator. All but the most energetic particles are deflected away by the Earth's magnetic field. Cosmic ray primaries enter the Earth's magnetic field before entering the atmosphere; the shape of this dipole field is such that both a latitude effect and an angular dependence (east-west effect) is present in its shielding properties. Since geomagnetic field lines are perpendicular to the Earth's surface at the poles, GCR particles have the tendency to be funneled towards these locations, while particles arriving near the equator are deflected away. From the poles to the equator, particles of increasingly high energy are prevented by the magnetic field from reaching the surface. This is referred to as the latitude effect. This magnetic deflection creates an asymmetry in the distribution of the arrival directions of cosmic ray particles entering the atmosphere. Moreover, positively charged particles—protons—arrive with greater abundance from the west than the east. This is referred to as the east-west effect [12]. The east-west effect accounts for a dominate proton component in the GCR spectrum.
The Earth's magnetic field, from the perspective of an incident GCR, can be understood in terms of a "stiffness" that varies with geomagnetic position. An incoming GCR can contribute to the radiation environment in the atmosphere only if the particle has sufficient momentum per unit charge, or rigidity, to penetrate the Earth's magnetic field and interact with air nuclei. That rigidity, which is a function of the particle's charge combined with the zenith and azimuthal angles its entrance makes with the Earth's surface, is called the cutoff rigidity and is expressed in gigavolts (GV), which is equivalent to GeV/c per unit charge. The rigidity is given by
| $\displaystyle{ R = \frac{p c}{Z e} \text{.} }$ | (2. |
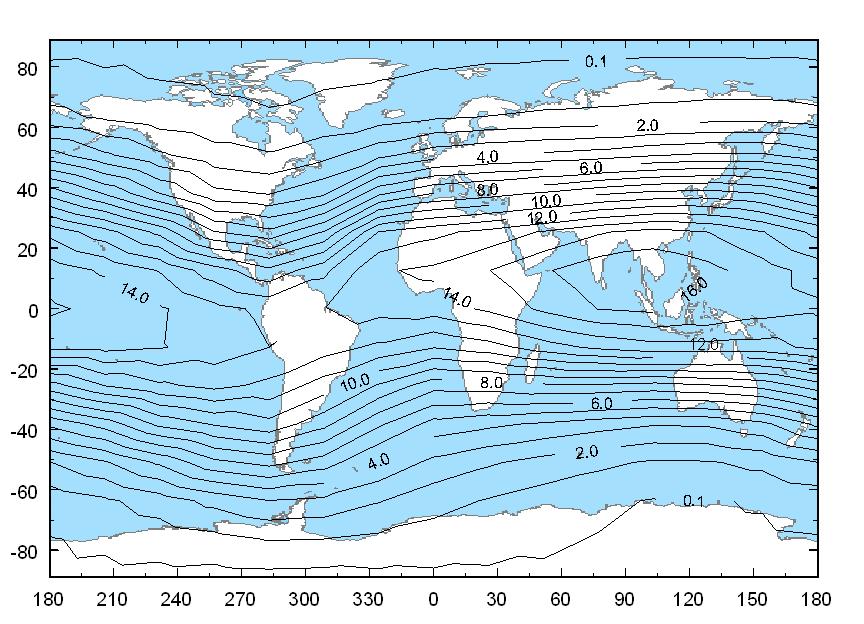
The Earth's magnetic field is characterized by a cutoff rigidity for a given geomagnetic position. It is a measure of the amount by which a particle of electric charge $Z$ and relativistic momentum $\mathbf{p} = \gamma m \mathbf{v}$ is deflected by a magnetic field. Particles of the same rigidity should be deflected by the same amount and therefore have similar trajectories in a given magnetic field configuration. The term "cutoff rigidity" refers to the ability of the Earth's magnetic field to act as a high-pass filter for incoming cosmic rays. Galactic cosmic rays usually arrive somewhat normal to the Earth's surface, and because of this, tables of vertical cutoff rigidities are compiled for a given magnetic epoch. The latitude effect and the east-west effect are illustrated by the contour plots of vertical cutoff rigidities in Figures 2.4 and 2.5 for solar minimum and solar maximum, respectively.

Interaction of GCRs with the Atmosphere
An incoming GCR can interact with the nuclei of the atmosphere once it has traversed the Earth's magnetic field. The particle can interact with air (or target) nuclei in two ways: 1) ionization and 2) nuclear fragmentation. Ionization is an electromagnetic phenomenon that results in the slowing of a charged particle when it interacts with electrons in the air that are also charged. Nuclear interactions, on the other hand, occur when a nucleon (a proton or neutron) interacts with a target nucleus, causing the production of secondary nucleons, pions, muons, and more. These interactions, both electromagnetic and nuclear, cease once the quantity of kinetic energy carried by the primary GCR has been dissipated.
Ionization vs. Nuclear Reactions
LET is the amount of energy deposited by a particle to the surrounding medium per unit path length, which is directly related to the amount of energy deposited per unit mass by electromagnetic processes (absorbed dose). LET is proportional to the square of the projectile charge, and inversely proportional to the square of the projectile velocity. A lower velocity translates into a higher LET, meaning that a particle is imparting more energy per unit path length to the medium (units: keV/μm).
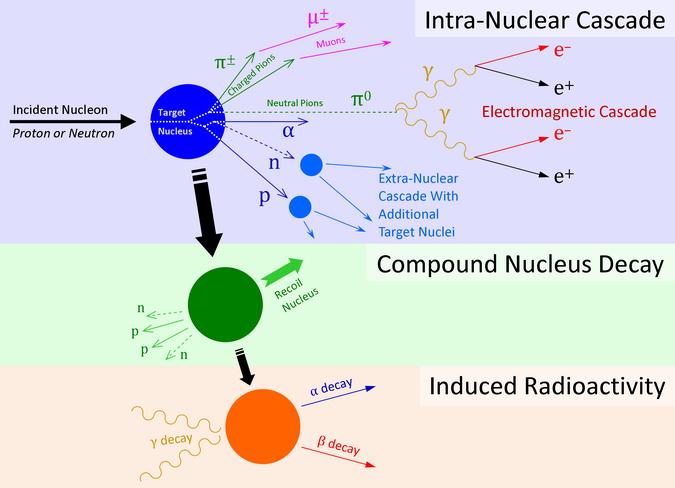
A classical picture of target fragmentation, shown in Figure 2.6, typically involves nucleon-nucleus reactions. The usual scenario involves the interaction of an incident proton or neutron with a target oxygen or nitrogen nucleus in the atmosphere. The incident nucleon is commonly a primary GCR proton, but a secondary proton or neutron resulting from an earlier nuclear interaction within the atmosphere may also be the case. A target fragmentation event can result in a number of different scenarios depending on the kinetic energy of the incident nucleon and the proximity of the interaction. For high energy interactions greater than 1 GeV, neutral and charged pions may be produced. Neutral pions quickly decay into gamma rays; these gamma rays can participate in pair production, provided they have enough energy to do so (~1.022 MeV). This leads to an electromagnetic cascade. Charged pions, on the other hand, undergo energy loss through ionization and can decay into charged muons, which themselves decay into electrons and positrons.
At intermediate energies above 50 MeV, the incident nucleon interacts with individual nucleons within the target nucleus, thereby producing knock-out protons, neutrons, alpha particles, and occasional light nuclei ($Z$ > 4). This is referred to as an intra-nuclear cascade. The emission of these nucleons during the cascade is usually in the forward direction. The emitted particles, having charge, will be slowed through ionization, but are still free to undergo additional nuclear interactions in what is known as an extra-nuclear cascade. The target nucleus is often left in an excited, unstable state—called a compound nucleus—after the initial collision and the resulting cascade. This compound nucleus can return to stability through the evaporation, or prompt emission, of protons, neutrons, and alpha particles. The evaporation of particles is nearly isotropic, with the nucleus recoiling in a direction conforming to conservation of momentum. These evaporation events of excited nuclei are more biologically damaging than energetic lightly ionizing particles.
The target nucleus may be in a final state of radioactivity following these events. Proton- or neutron-induced radioactivity will require either alpha, beta, or gamma decay to achieve stability in the long term (i.e., a time frame measured in seconds). The radioactive decay products will be emitted nearly isotropically, as in the case of the compound nucleus.
III. Air Showers


The ionizing radiation environment at all but the lowest altitudes is composed almost entirely of secondary particles. These secondary particles arise from air showers or particle cascades initiated when a primary cosmic ray interacts with a constituent nucleus of the atmosphere. Earth's atmosphere is sufficiently dense that a significant portion of the primary cosmic ray flux will undergo nuclear in addition to electromagnetic interactions. This results in the production of large quantities of secondary particles. The particle cascade will conclude its development when the kinetic energy possessed by the incident cosmic ray has been depleted by the atmosphere.

The trajectories of the secondary particles produced in an air shower are similar to that of the primary cosmic ray. These secondaries are electromagnetically scattered as they propagate through the atmosphere, while others are emitted isotropically (in the particle's frame of reference) after a nuclear interaction. Many secondary particles have sufficient energy to undergo further nuclear reactions. In this manner several generations of secondaries are produced—especially nucleon cascades—which can extend to sea level if the incident primary has an energy greater than about 500 MeV. The superposition of angular and spatial behaviors inherent in the development of a particle cascade yields a cone shape for the air shower. The apex of this cone marks the entry point of the primary cosmic ray into the atmosphere; the air shower widens as it develops from higher to lower altitudes. Figure 3.1 illustrates an air shower initiated by a high energy proton.

The Pfotzer maximum, depicted in the Figure 3.2, is a region located at an altitude of about 20 km (with a width of about 8-10 km) where the secondary particle flux is greatest. The Pfotzer maximum arises from the competition of secondary particle production by ionization and nuclear processes. Above the Pfotzer maximum, secondary particle production dominates since the incoming cosmic rays contain enough energy to fuel this via nuclear interactions. In this region, energy loss through ionization is dominated by nuclear processes. Below the Pfotzer maximum, however, the converse is true: the particle flux is attenuated via ionization. More specifically, the energy contained within a given air shower is no longer sufficient to maintain secondary particle production via nuclear interactions.
Most of the momentum is carried in the forward (or longitudinal) direction during nuclear reactions in the atmosphere; at sufficiently high energies the transverse momentum can be neglected, thus simplifying these reactions to a "straight-ahead" or one‑dimensional problem. In this case the net loss of particles involved in nuclear reactions at altitudes below the Pfotzer maximum can be expressed in terms of a quantity called the particle mean free path. The particle mean free path combines particle creation and absorption processes into a single parameter $L$:
| $\displaystyle{ I_2[\text{cm}^{-2} \space \text{s}^{-1} \space \text{MeV}^{-1}] = I_1 \mathrm{e}^{(X_1 - X_2) / L} \text{,} }$ | (3. |
where $I_1$ is the flux at a lower altitude $X_1$ than altitude $X_2$ with a flux of $I_2$. Table 3.1 contains typical mean free path values for a variety of particles found in air showers.
| Particle | Mean free path (g/cm2) |
|---|---|
| Electron | 100 |
| Proton Pion |
110 |
| Neutron | 148 |
| Muon | 520 |
Since the interaction strength with the atmosphere and mass differ between particles in the above table, so do the mean free paths. It should be noted that a secondary's loss of kinetic energy only by electromagnetic means is very low per unit path length through the atmosphere. This translates into much longer mean free paths than those listed in Table 3.1.
The particle cascade (or air shower) initiated by a primary cosmic ray entering the atmosphere has three components: hadronic, electromagnetic, and muonic. Each of these components is a distinct interaction process even though they are physically related. The population of secondary particles, which are halted primarily through ionization, are created in the upper atmosphere as a result of these three processes. With the exception of muons and their decay products (electrons), and to a lesser extent neutrons, the vast majority of an air shower yield is attenuated through ionization before reaching the Earth's surface. This is because the path length between successive electromagnetic or nuclear interactions decreases, which is attributed to the exponential density increase of the atmosphere with lower altitudes. As a result, the rate of ionization increases when approaching the surface of the Earth.
Hadronic Component
Hadronic cascades involve nuclear interactions between hadrons via the strong force, producing secondaries that initiate and feed the succeeding electromagnetic and muonic cascades. The hadrons of interest in this case include protons and neutrons (nucleons), alpha particles (helium nuclei), and heavy nuclei. An air shower begins when a primary cosmic ray (e.g., proton) interacts with a nitrogen or oxygen nucleus in the upper atmosphere. Upon entering the atmosphere, nuclear interactions occur (on average) after traversing about 70 g/cm2 depth of atmosphere for protons, and about 25 g/cm2 for alpha particles [12]. A hadronic interaction initiated by a proton reads:
| $\displaystyle{ \text{p} + \text{Air} \to N_\text{n} \text{n} + N_\text{p} \text{p} + N_{\pi^\pm} \pi^\pm + N_{\pi^0} \pi^0 + N_\gamma \gamma \text{.} }$ | (3. |
Substituting the proton with a secondary neutron produced in an earlier interaction in left side of Equation (3.2) will leave it unchanged. The multipliers $N_i$ can be equal to any integer value in Equation (3.2) with the result that a great variety of product combinations may result from any one reaction. After muons, the next most abundant elementary particles detected at sea level are neutrons. Atmospheric neutrons are highly penetrating since they are non-ionizing and have a relatively long mean lifetime of approximately 12 minutes. Just as many protons as neutrons are produced in cosmic ray air showers, but since secondary protons stop at high altitudes through ionization, they are not detected at sea level. This is in contrast to secondary neutrons, of which small numbers are detected with dedicated ground level neutron monitors.
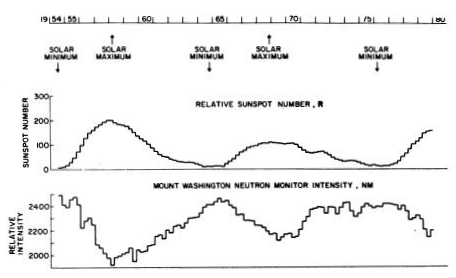
Neutron monitors at various locations around the world are used to measure the cosmic ray flux incident on the Earth's atmosphere. A neutron monitor is a ground-level device that is sensitive to the secondary neutrons present in air showers caused by cosmic rays at the top of the atmosphere. In terms of the placement of a neutron monitor, a lower geomagnetic cutoff rigidity gives a better indication of the cosmic ray flux incident at the top of the atmosphere. For example, the Mount Washington Neutron Monitor data shown in Figure 3.3 displays good anti-correlation between the relative sunspot number and neutron monitor intensity. This indicates that the greater the level of solar activity, the more effective the solar wind is in preventing the interstellar flux of cosmic rays from reaching the Earth. This adjustment is referred to as solar modulation. It should also be noted that Figure 3.3 shows data for two solar cycles, where one solar cycle is defined as the 11‑year period during which the sunspot number and general solar activity goes from minimum to maximum, then back to minimum.
Electromagnetic Component
Electromagnetic cascades are largely the result of the decay of neutral pions ($\pi^0$) originally produced in high energy hadronic reactions. Neutral pions yield a pair of high energy photons (gamma rays) as their decay products after a very short time interval of approximately 10-17 seconds:
| $\displaystyle{ \pi^0 \to 2 \gamma \text{.} }$ | (3. |
A gamma ray will undergo pair production via conservation of energy:
| $\displaystyle{ E_\gamma = E_+ + m_\text{e} c^2 + E_- + m_\text{e} c^2 + E_\text{recoil} \text{.} }$ | (3. |
resulting in the formation of a positron-electron pair:
| $\displaystyle{ \gamma \to \text{e}^+ \text{e}^- \text{.} }$ | (3. |
In Equation (3.4), $E_+$ and $E_-$ are the energies of the positron and electron, respectively, and $E_\text{recoil}$ is the energy imparted to a nearby massive nucleus. A massive charged object is required in order to satisfy conservation of momentum, since both the photon and the nucleus are producing an electromagnetic field. The minimum energy requirement for pair production is taken from the rest mass of the positron/electron:
| $\displaystyle{ E_\gamma = 2 m_\text{e} c^2 = 2(0.51 \text{ MeV} / c^2) c^2 = 1.02 \text{ MeV.} }$ | (3. |
Excess photon energy above 1.02 MeV appears as the kinetic energy of the pair plus the recoil of the nucleus, which is so small as to be negligible. The created positron will eventually annihilate with a free electron in the atmosphere, producing two gamma rays:
| $\displaystyle{ \text{e}^+ + \text{e}^- \to 2 \gamma \text{.} }$ | (3. |
The pair-production-to-annihilation process will continue provided a gamma ray has sufficient energy to do so. In general, pair production is important only for photons of energy above 5 MeV.
Muonic Component
Muonic cascades are the result of the decay of charged pions ($\pi^\pm$) produced in hadronic reactions:
| $\displaystyle{ \pi^+ \to \mu^+ + \nu_\mu \text{,} }$ | (3. |
| $\displaystyle{ \pi^- \to \mu^- + \bar{\nu}_\mu \text{.} }$ | (3. |
Charged pions are created at a mean depth of about 125 g/cm2 in the atmosphere and are very short lived, with a mean lifetime of approximately 26 ns at sea level there is approximately 1 charged pion per 1000 muons. Charged muons ($\mu^\pm$) are long range, minimally ionizing particles, and so are one of the few particles that can be readily detected near the Earth's surface. The muons themselves may also decay:
| $\displaystyle{ \mu^+ \to \text{e}^+ + \bar{\nu}_\mu + \nu_\text{e} \text{,} }$ | (3. |
| $\displaystyle{ \mu^- \to \text{e}^- + \nu_\mu + \bar{\nu}_\text{e} \text{.} }$ | (3. |
The electron and muon neutrinos ($\nu$), together with their associated antiparticles ($\bar{\nu}$), are non-ionizing and weakly interacting, and therefore their contribution to the atmospheric radiation environment can be neglected.

At sea level, the most abundant cosmic ray secondary particles are muons. Muons behave like massive electrons except that they are unstable and have a mean lifetime of approximately 2 μs. Because of this short lifetime, the detection of air shower muons at or near sea level is an excellent demonstration of special relativity. The first observation of secondary cosmic ray muons dates back to the 1940s, when ionization chambers were used. Over time, the detection technique migrated to the use of Geiger-Müller counters, then finally to plastic scintillators. A muon detector using slabs of plastic scintillator ("paddles") employs a coincidence technique to deduce the arrival of an ionizing muon. A muon detector utilizing two or more paddles is called a muon "telescope" because the scintillator paddles are arranged in the same way as lenses in an optical telescope.
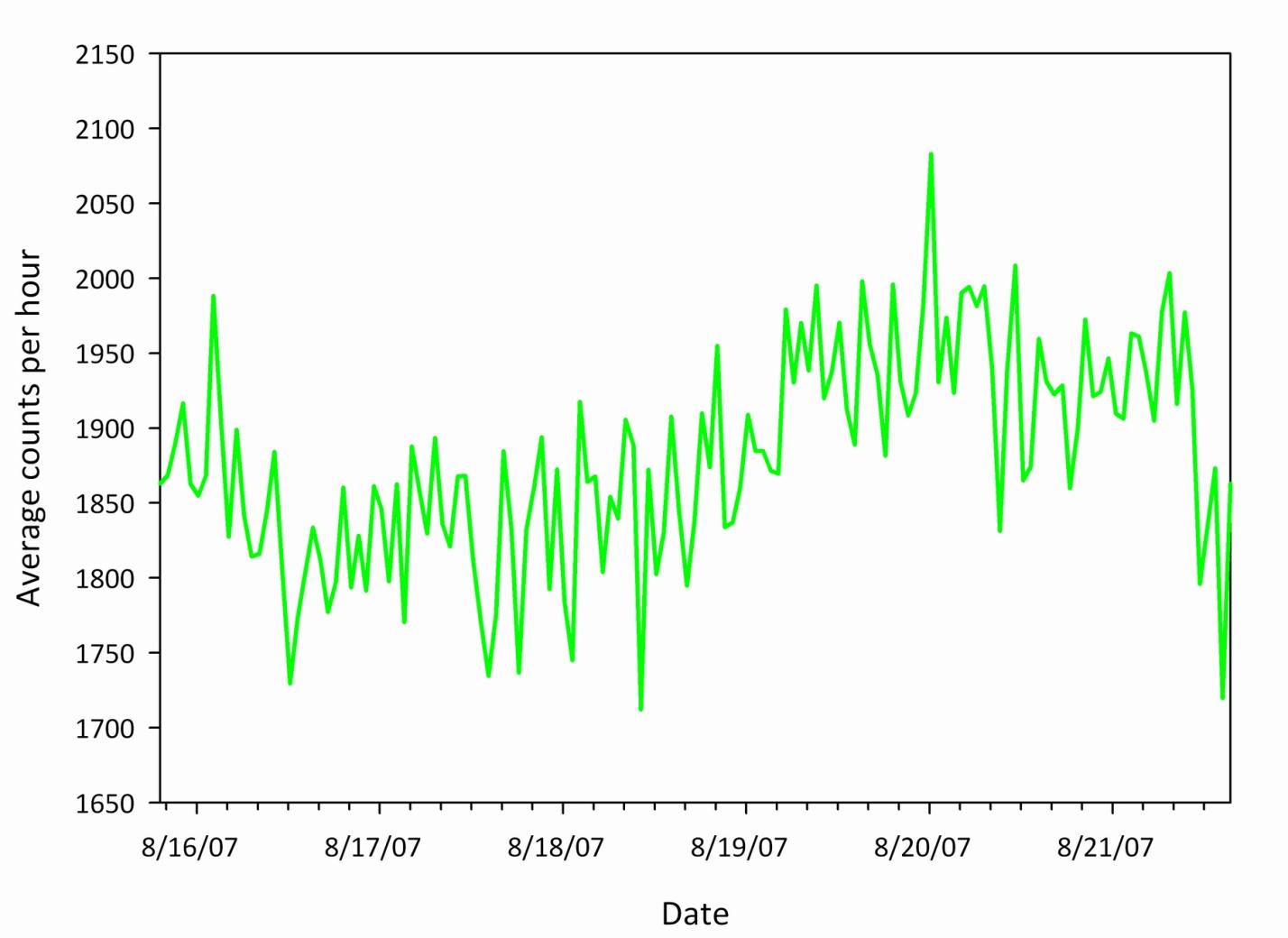
Modern muon telescopes are simple ionizing radiation detectors arranged in two or more paddles. These detector systems produce output pulses on the order of 1 ms whenever a charged particle passes through them. Since the incoming muon is traveling relativistically, and crossing the complete telescope before the electronics are able to register its passage, a simple coincidence technique must be employed in order to detect the particle. Several muon telescopes have been constructed by Carl Johnson of the OSU Radiation Physics Laboratory and have been operational since the middle of 2007 [20]. Sample total muon count rate measurements ($\mu^+$ + $\mu^-$) made by these detection systems are presented in Figures 3.4 and 3.5.
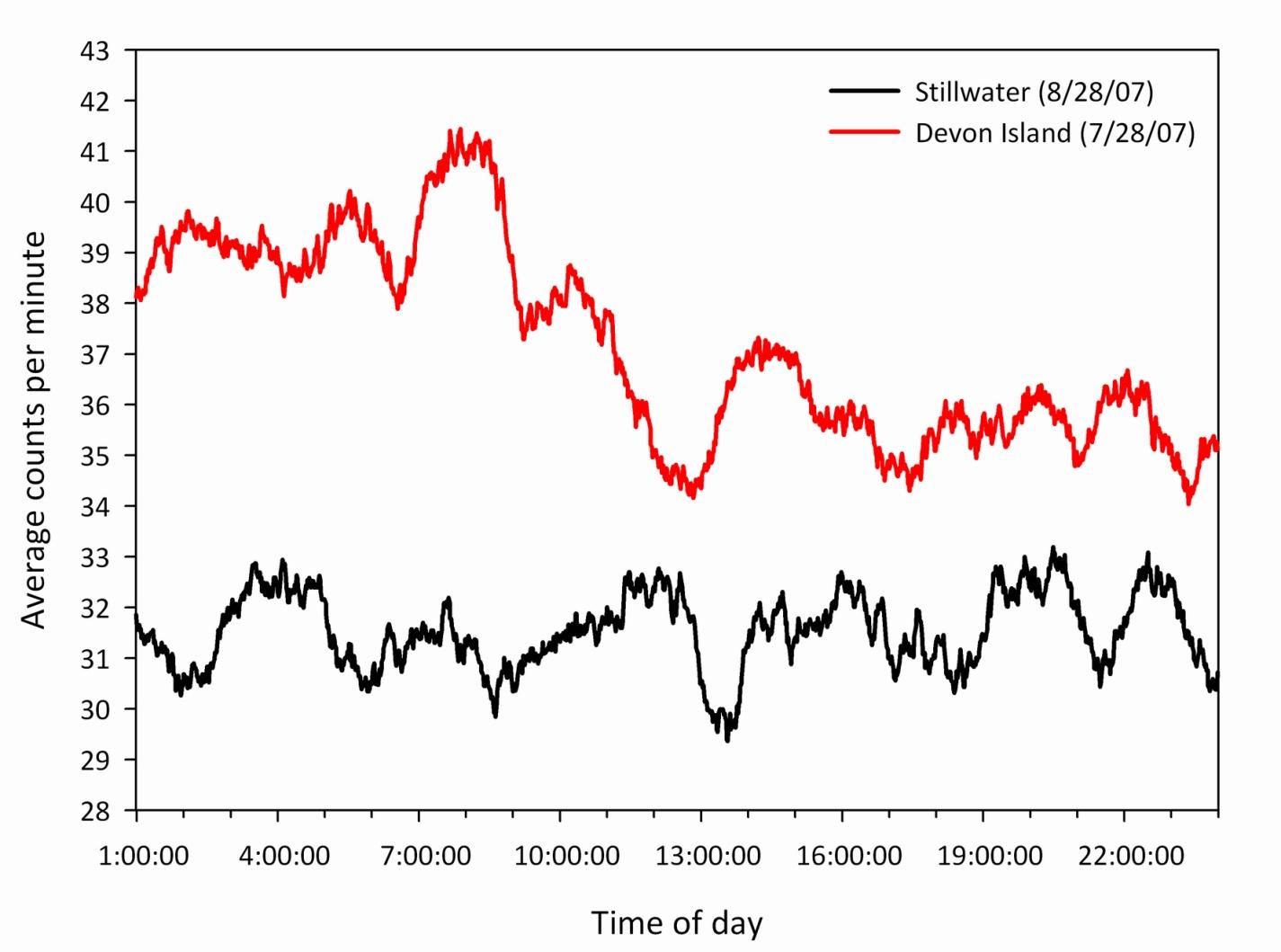
The opportunity to send a portable muon detector to a high geomagnetic latitude in the summer months of 2007 enabled the collection of muon data to compare to that from the Stillwater latitude. A comparison of these data over a 24‑hour period is shown in Figure 3.6. The higher count rate measured on Devon Island illustrates the latitude effect of a location with a higher geomagnetic latitude. A higher geomagnetic latitude, in general, corresponds to a lower vertical cutoff rigidity, effectively reducing the protection the Earth's magnetic field offers. Physically this lowered cutoff translates into a reduced momentum-per-unit-charge requirement of a primary cosmic ray to enter the Earth's atmosphere and initiate an air shower, creating secondary muons as a result.
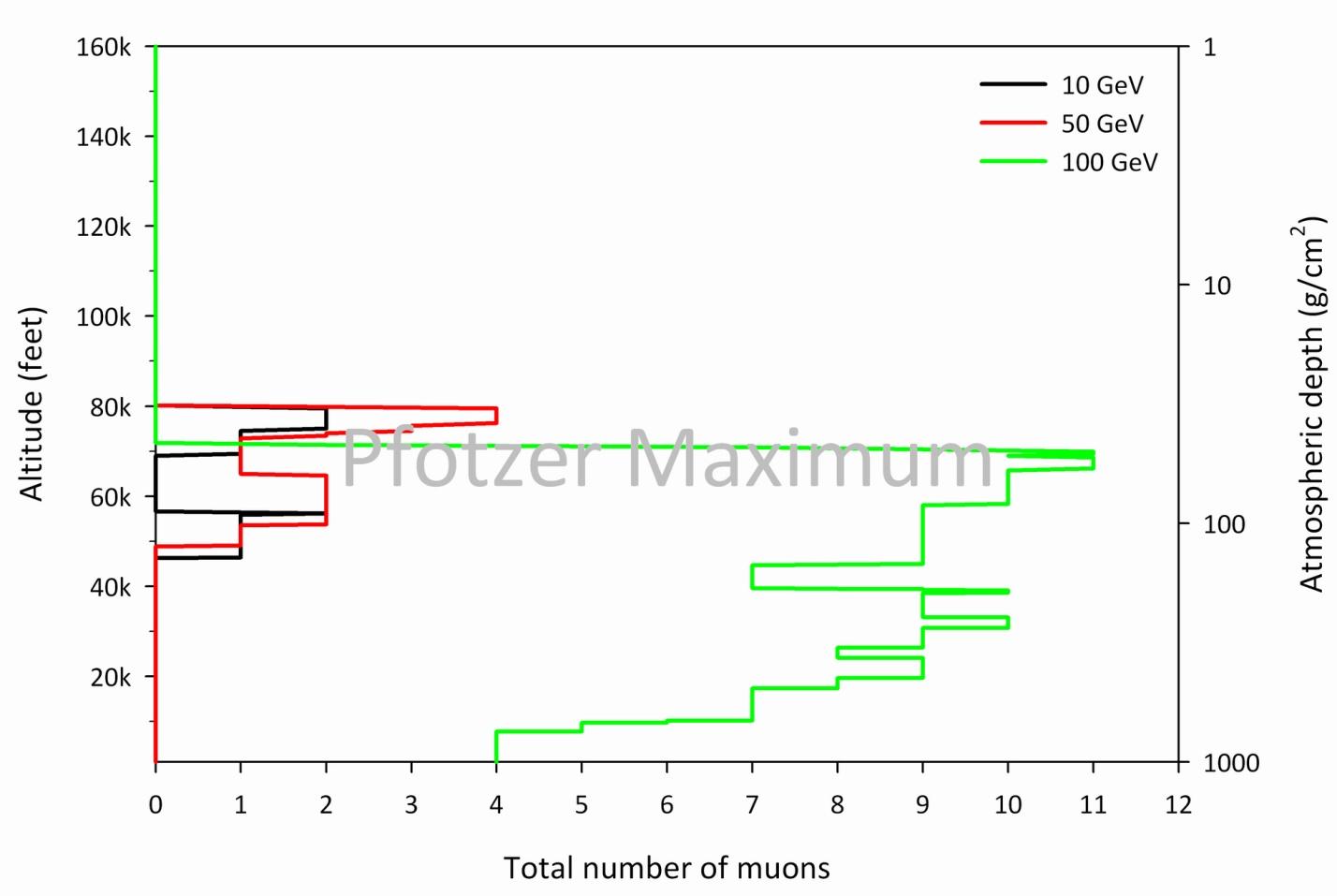
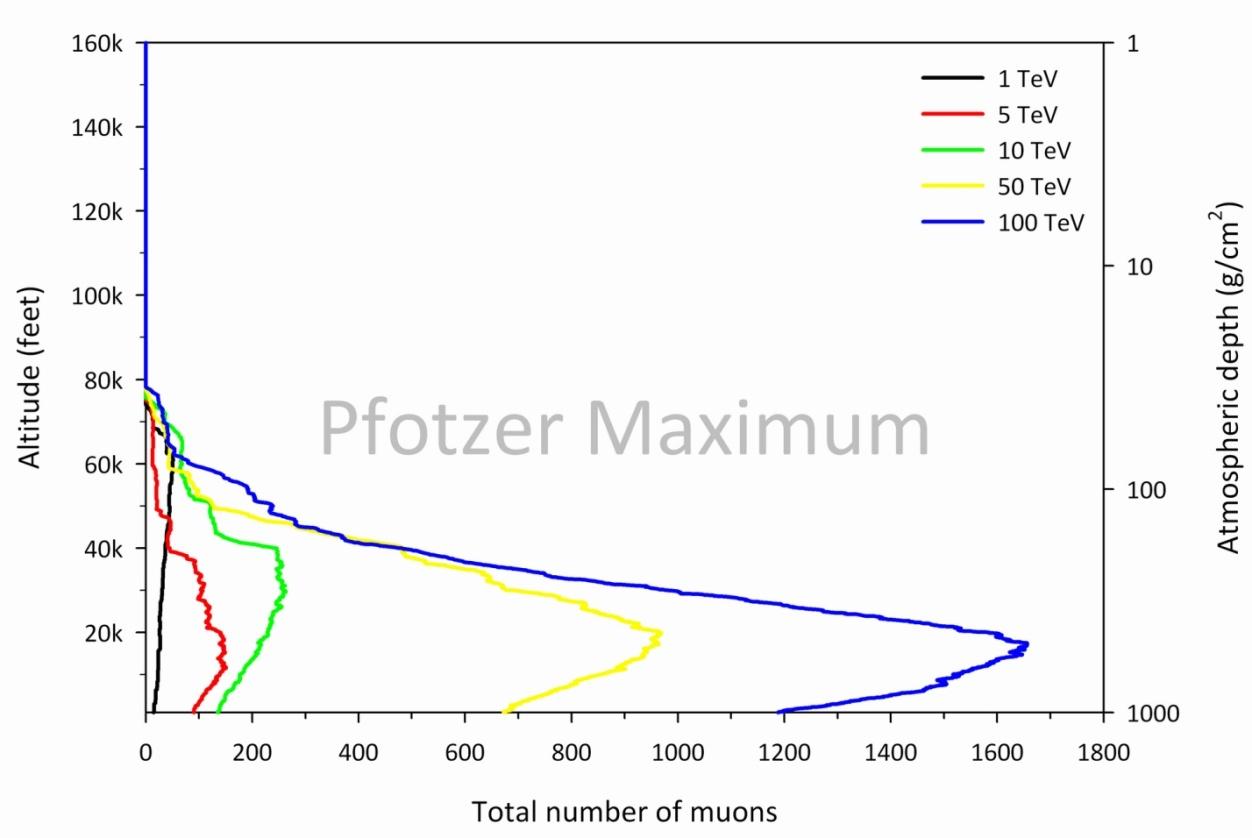
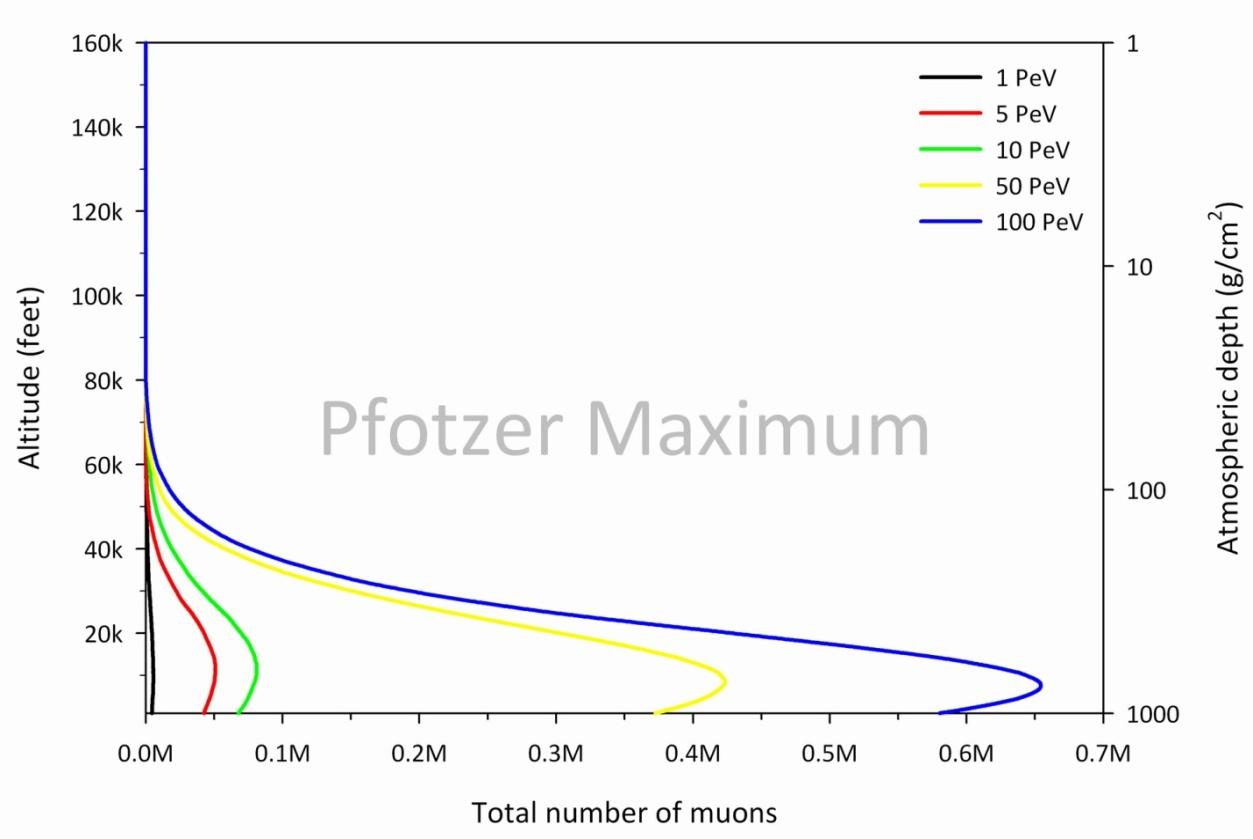
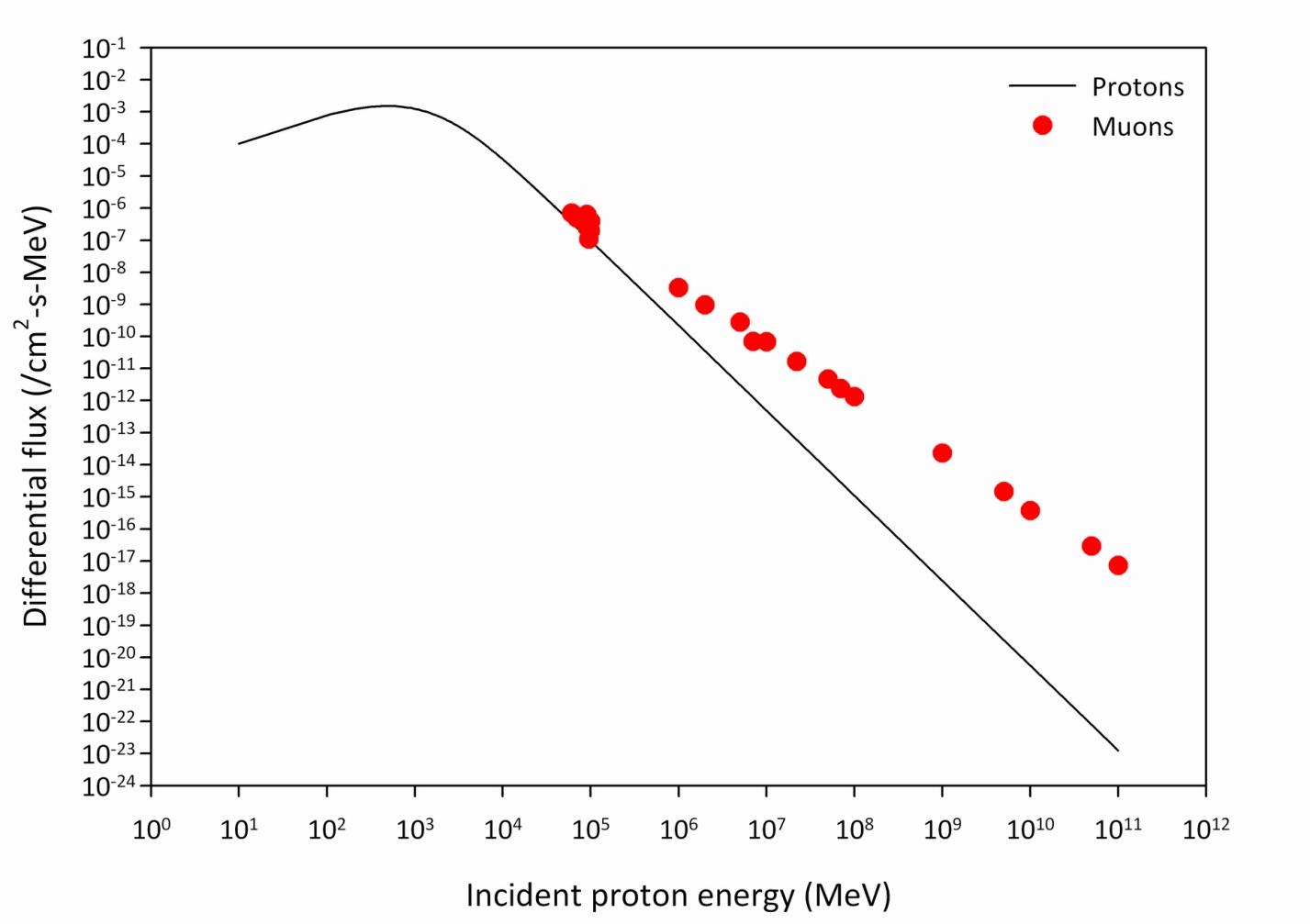
To complement our laboratory's muon measurements, I used a Monte Carlo computer code called COsmic Ray SImulations for KAscade (CORSIKA) to model the reaction $\pi^\pm \to \mu^\pm + \nu$ in the atmosphere. This step was taken in order to answer the question: What primary proton energies are responsible for most of the muons detected by the muon telescope? Figure 3.7, Figure 3.8, and Figure 3.9 show simulated total muon production ($\mu^+$ + $\mu^-$) in the Earth's atmosphere for GeV, TeV, and PeV incident GCR proton energy regimes, respectively. Figure 3.7 shows a peak total muon count corresponding the Pfotzer maximum (about 58 g/cm2 or 66,000 feet) for the 100 GeV proton. However, this is not the case for high incident proton energies (Figure 3.8 and Figure 3.9), where peak total muon counts occur at significantly lower altitudes. This suggests that, while incident protons with lower kinetic energies in the GeV range initiate air showers that produce far fewer muons, they are much more frequent and hence are responsible for the muonic component of the Pfotzer maximum. Figure 3.10 shows a comparison of the results depicted in Figure 3.7, Figure 3.8, and Figure 3.9, where the individual data points in Figure 3.10 are the total number of muons to reach sea level. This trend is shown alongside the result of a proton energy spectrum model at the top of the atmosphere. A comparison of these data reveals that frequent lower energy protons initiating air showers at the top of the Earth's atmosphere produce a greater flux of muons that reach sea level. This is in contrast to much higher energy protons that occur less frequently but produce large quantities of muons. This rarity of high energy protons translates into a reduced flux of muons that can be detected at sea level. In other words, while roughly 100 GeV protons create far fewer muons than higher energy protons, they are so much more numerous that they lead to the majority of secondary muons detected near sea level.
Footnotes
- E.R. Benton, E.G. Yukihara, A.S. Arena, Jr., and A.C. Lucas, Tissue Equivalent Detectors for Space Crew Dosimetry and Characterization of the Space Radiation Environment, A NASA Experimental Program to Stimulate Competitive Research (EPSCoR) Project (2007).Back to standard weather balloons
- W. Heinrich, S. Roesler, and H. Schraube, "Physics of Cosmic Radiation Fields," Radiation Protection Dosimetry 86(4), 253 (1999).Back to natural background radiation
- E.A. Blakely, "Biological Effects of Cosmic Radiation: Deterministic and Stochastic," Health Physics 79(5), 495 (2000).Back to 600 hr/yr exposure time
- F. Spurný and Ts. Dachev, "Measurements in an Aircraft during an Intense Solar Flare, Ground Level Event 60, on April 15, 2001," Radiation Protection Dosimetry 95, 273 (2001).Back to average person at sea level
- E. Ron, "Ionizing Radiation and Cancer Risk: Evidence from Epidemiology," Radiation Research 150, S30 (1998).Back to fatal cancer
- V. Rafnsson, E. Olafsdottir, J. Hrafnkelsson, H. Sasaki, A. Arnarsson, and F. Jonasson, "Cosmic Radiation Increases the Risk of Nuclear Cataract in Airline Pilots," Arch Ophthalmol. 123(8), 1102 (2005).Back to cataracts in the eyes
- T. Foelsche, R.B. Mendell, J.W. Wilson, and R.R. Adams, "Measured and Calculated Neutron Spectra and Dose Equivalent Rates at High Altitudes; Relevance to SST Operations and Space Research," NASA Technical Note D-7715 (1974).Back to near solar maximum
- J.A. Simpson, "Elemental and Isotropic Composition of the Galactic Cosmic Rays," Annual Review of Nuclear and Particle Science 33, 323 (1983).Back to broken down as follows
- E.R. Benton, "Radiation Dosimetry at Aviation Altitudes and in Low-Earth Orbit," PhD dissertation (2004).Back to adapted from
- G.D. Badhwar, "The Radiation Environment in Low-Earth Orbit," Radiation Research 148, S3 (1997).Back to model calculation
- G.D. Badhwar and P.M. O'Neill, "An Improved Model of Galactic Cosmic Radiation for Space Exploration Missions," Nuclear Tracks and Radiation Measurements 20, 403 (1992).Back to time-dependent solar adjustment of the GCR spectrum
- B. Rossi, Cosmic Rays, New York, McGraw-Hill (1964).Back to latitude effect
- T.H. Johnson, "A Note on the Nature of the Primary Cosmic Radiation," Physical Review 54, 385 (1938).Back to dominate proton component in the GCR spectrum
- E.R. Benton, personal communication (2008).Back to taken from
- K. O'Brien and J.E. McLaughlin, "The Radiation Dose to Man from Galactic Cosmic Rays," Health Physics 22, 225 (1972).Back to one‑dimensional problem
- J.F. Ziegler, "Terrestrial cosmic rays," IBM Journal of Research and Development 40, 19 (1996).Back to particle mean free path
- M.A. Shea and D.F. Smart, "An update on the correlation between the cosmic radiation intensity and the geomagnetic AA index," Proceedings of the 19th International Cosmic Ray Conference 4, 501 (1985).Back to taken from
- K.S. Krane, Introductory Nuclear Physics, pg. 201 (1988).Back to above 5 MeV
- M.L. Duldig, "Muon Observations," Space Science Reviews 93, 207 (2000).Back to about 125 g/cm2 in the atmosphere
- C. Johnson, personal communication (2008).Back to as measured in Stillwater
- D. Heck, J. Knapp, J.N. Capdevielle, G. Schatz, and T. Thouw, "CORSIKA: A Monte Carlo Code to Simulate Extensive Air Showers," Forschungszentrum Karlsruhe Report FZKA 6019 (1998).Back to in the atmosphere
- R.C. Reedy, "Nuclide production by primary cosmic-ray protons," Journal of Geophysical Research 92, E697 (1987).Back to top of the atmosphere


